主要参考liweiwei1419的题解以及下方评论
关于快速排序的总结也是参考liweiwei1419的《算法不好玩》专题六:快速排序
下面有一段无关标题的废话要说,不想看直接点击跳过
1 摘要
前天写完十个经典排序的博客后就寻思找几个题试试手,结果找到了力扣的215. Kth Largest Element in an Array (Medium),结果证明自己还是太年轻,不过经过努力奋斗,对优先队列,堆排序,选择排序的有了更深一步的认识。
1.1 优先队列是没啥好说的,主要使用到Java的PriorityQueue(小顶堆),出队,入队已经封装好了、调整堆的过程已经省去,只要调用就行;贴一个题解:
1
2
3
4
5
6
7
8
9
10
11
| public int findKthLargest(int[] nums, int k) {
PriorityQueue<Integer> pq = new PriorityQueue<>();
for (int val : nums) {
pq.add(val);
if (pq.size() > k)
pq.poll();
}
return pq.peek();
}
|
1.2再就是基于堆排序,不了解堆排序的可以参考堆排序(Heap Sort),主要是建堆、调整堆,也贴一个题解:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
| public int findKthLargest(int[] nums, int k) {
buildMaxHeap(nums);
for(int i = 1; i < k; i++){
swap(nums, 0, nums.length - i);
adjustHeap(nums, 0, nums.length - i);
}
return nums[0];
}
private void buildMaxHeap(int[] nums){
int start = nums.length / 2 - 1;
for(int i = start; i >= 0; --i){
adjustHeap(nums, i, nums.length);
}
}
private void adjustHeap(int[] nums, int parent, int high){
int left = parent * 2 + 1;
int right = parent * 2 + 2;
int largest = parent;
if(right < high && nums[largest] < nums[right]){
largest = right;
}
if(left < high && nums[largest] < nums[left]){
largest = left;
}
if(largest != parent){
swap(nums, parent, largest);
adjustHeap(nums, largest, high);
}
}
private void swap(int[] nums, int index1, int index2){
int temp = nums[index1];
nums[index1] = nums[index2];
nums[index2] = temp;
}
|
1.3 快速选择
节省点篇幅,主要是讲快速排序而不是快速选择的[狗头],看题解吧
https://leetcode.cn/problems/kth-largest-element-in-an-array/solution/partitionfen-er-zhi-zhi-you-xian-dui-lie-java-dai-/
2 快速排序
以力扣912. 排序数组作为性能评判标准
2.1 单方向遍历快排
详情可见2.6 快速排序(Quick Sort)
代码如下
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
| class Solution {
public int[] sortArray(int[] nums) {
quickSort(nums, 0, nums.length - 1);
return nums;
}
private void quickSort(int[] nums, int left, int right){
if(left < right){
int pivotIndex = partition(nums, left, right);
quickSort(nums, left, pivotIndex - 1);
quickSort(nums, pivotIndex + 1, right);
}
}
private int partition(int[] nums, int left, int right){
int pivot = nums[left];
int index = left + 1;
for(int i = left + 1; i <= right; i++){
if(nums[i] < pivot){
swap(nums, i, index);
index++;
}
}
swap(nums, left, --index);
return index;
}
private void swap(int[] arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
|
效率,很不幸,超时

超时要向出改进方法,快速排序要求数组的顺序越随机越好
- 问题:对于顺序数组或者逆序数组来说,递归树高度增加、递归树倾斜;
- 再提出解决方案:破坏顺序性,随机选择 pivot。
快速排序对于有序的数组并没有那么友好

避免这种最坏的情况出现,我们在切分 partition 之前,只需要在待排序的区间里,随机选择一个元素交换到数组的第 1 个位置就可以了,这样,最坏的情况出现的概率就极其低了。
针对特殊测试用例(顺序数组或者逆序数组)一定要随机化选择切分元素(pivot),否则在输入数组是有序数组或者是逆序数组的时候,快速排序会变得非常慢(等同于冒泡排序或者「选择排序」)。
优化:随机选择标定点元素,降低递归树结构不平衡的情况
由于快速排序在近乎有序的时候会非常差,此时递归树的深度会增加。此时快速排序的算法就退化为 `O(N^2)。
解决办法:我们在每一次迭代开始之前,随机选取一个元素作为基准元素与第 1 个元素交换即可。
改进后代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
| class Solution {
private static final Random RANDOM = new Random();
public int[] sortArray(int[] nums) {
quickSort(nums, 0, nums.length - 1);
return nums;
}
private void quickSort(int[] nums, int left, int right){
if(left < right){
int pivotIndex = partition(nums, left, right);
quickSort(nums, left, pivotIndex - 1);
quickSort(nums, pivotIndex + 1, right);
}
}
private int partition(int[] nums, int left, int right){
int randomIndex = RANDOM.nextInt(right - left + 1) + left;
swap(nums, left, randomIndex);
int pivot = nums[left];
int index = left + 1;
for(int i = left + 1; i <= right; i++){
if(nums[i] < pivot){
swap(nums, i, index);
index++;
}
}
swap(nums, left, --index);
return index;
}
private void swap(int[] arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
|
性能:

2.2 双路快排
当数组中有很多值相同元素的时候,此时随机选择一个元素来与首位值来交换,这样很容易选到和首位相同的数,这样的交换是没有意义的
解决办法:
双路快排:把和pivot相等的值平均分配到数组两侧
三路快排:把和pivot相等的值放在数组中间
这里讲解双路快排
参考代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
| class Solution {
private static final Random RANDOM = new Random();
public int[] sortArray(int[] nums) {
quickSort(nums, 0, nums.length - 1);
return nums;
}
private void quickSort(int[] nums, int left, int right){
if(left < right){
int pivotIndex = partition(nums, left, right);
quickSort(nums, left, pivotIndex - 1);
quickSort(nums, pivotIndex + 1, right);
}
}
private int partition(int[] nums, int left, int right){
int randomIndex = RANDOM.nextInt(right - left + 1) + left;
swap(nums, left, randomIndex);
int pivot = nums[left];
int low = left + 1, high = right;
while(true){
while(low <= high && nums[low] < pivot){
++low;
}
while(low <= high && nums[high] > pivot){
--high;
}
if(low >= high){
break;
}
swap(nums, low, high);
++low;
--high;
}
swap(nums, left, high);
return high;
}
private void swap(int[] arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
|
性能分析:快了不只一个档次

2.3 三路快排
三路快排就是将等于pivot的数字都放在数组中间,这样就只需要对大于和小于pivot值进行递归排序了,如果当划分值等于大量重复的值的时候,可以大大减少排序区间
weiwei哥的视频讲的更加详细,截了几张图,帮助自己加深印象

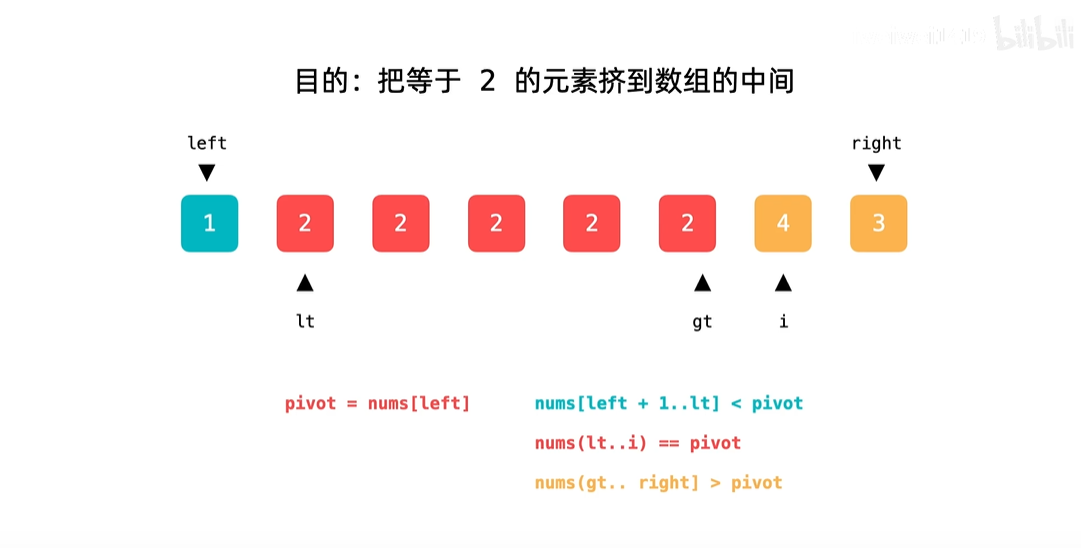
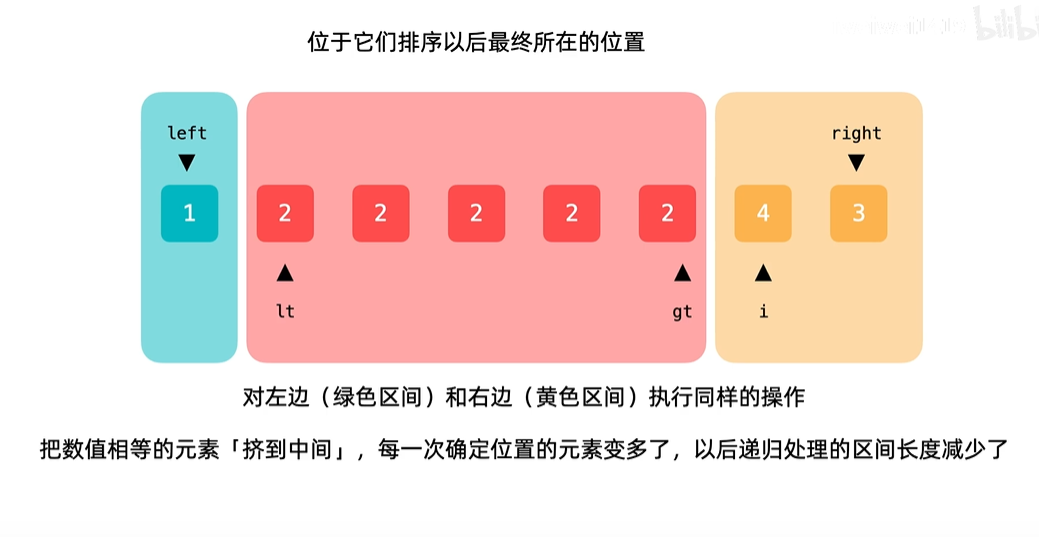
代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
| class Solution {
private static final Random RANDOM = new Random();
public int[] sortArray(int[] nums) {
quickSort(nums, 0, nums.length - 1);
return nums;
}
private void quickSort(int[] nums, int left, int right){
if(left < right){
int randomIndex = RANDOM.nextInt(right - left + 1) + left;
swap(nums, left, randomIndex);
int pivot = nums[left];
int low = left + 1, high = right;
int i = left + 1;
while(i <= high){
if(nums[i] < pivot){
swap(nums, i, low);
++i;
++low;
}else if(nums[i] == pivot){
++i;
}else{
swap(nums, i, high);
--high;
}
}
swap(nums, left, low - 1);
quickSort(nums, left, low - 2);
quickSort(nums, high + 1, right);
}
}
private void swap(int[] arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
|
性能分析:和二路快排差不多,慢了一点,可能是没有很多重复值的测试用例

3 总结
一般情况只需要掌握二路快排就够了,但是三路快排的思想要掌握,且在一些特殊情况很有用,如很多重复值的数组排序,贴一张截图,完成快速排序学习!!!









